A Trig-less Line of Sight Algorithm in Two Dimensions
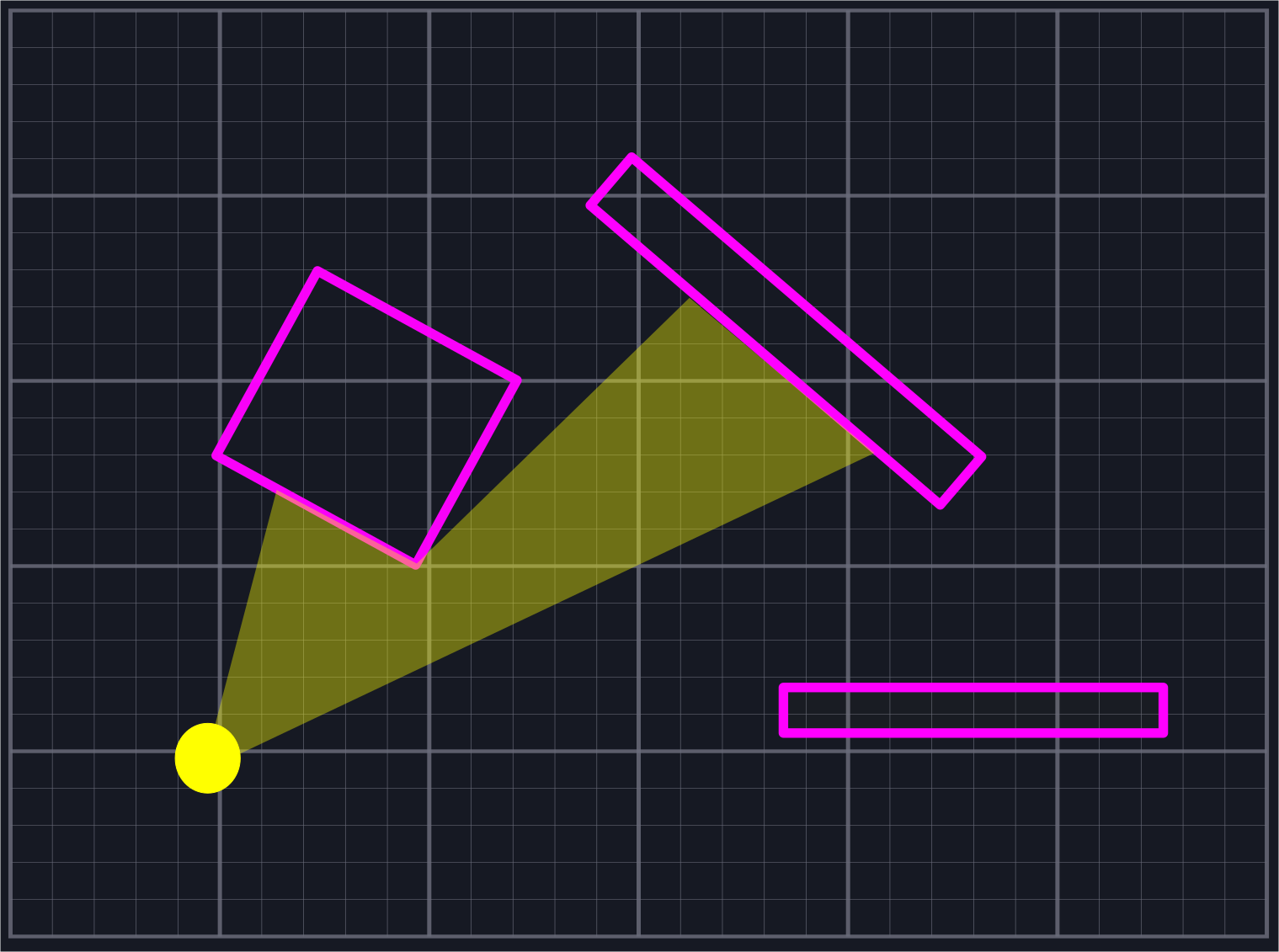
It is common when simulating two-dimensional worlds (i.e. for video games) to want to determine line of sight from a specific point \(P\). That is, we'd like to find (a reasonable approximation to) the set of points \(Q\) such that the line \(\vec{PQ}\) does not pass through any solid objects. There are a few great articles that already talk about various approaches to this problem. In particular, the three linked below in the references section were used in various capacities during the formulation of the approach given here.
There are two theoretical complaints one might raise about the existing implementations. Firstly, one method purposefully excludes small slices of area that should be marked as visible near corners of wall segments. Secondly, they often feature (potentially) expensive operations such as (inverse) trigonometric functions or square roots, and the explanations of portions of the algorithm can lack intuition. In practice, these generally run quickly enough for what we need. Just because a given operation is expensive in theory doesn't mean that an alternate approach avoiding it will be faster in practice. Additionally, close enough is generally good enough for most use cases. All that being said, however, it is still worthwhile to see what can be done to address these concerns.
As such, we give an algorithm here which we attempt to explain in straightforward fashion using vectors. It only uses the operations of basic arithmetic: addition, subtraction, multiplication, and a few divisions. This is intended more as an exercise in using vectors rather than any attempts to create production ready code. Familiarity with vector basics such as vector addition, subtraction, and the dot product will be necessary. I recommend that serious projects use one of the algorithms listed in the references, as they are likely to be more battle-tested and stable. Here we do not handle floating point errors with much care, and we could signifcantly improve how we sort and iterate through structures.
The repository contains the code for our algorithm and a simple example application built using the ggez crate. The code samples are written in Rust, however our code should be relatively language-agnostic for anyone with some experience with C-style syntax.